DSP envelopes
The envelope value of each S-DSP voice is driven by either an ADSR envelope, or a gain control. This gives an additional way to automatically shape the volume of the voice over time, aside from its VOL registers.
Internally the envelope is an 11-bit value multiplied by by the voice output. The ENVX value that can be read from the DSP contains only the high 7 bits.
See:
ADSR Envelope
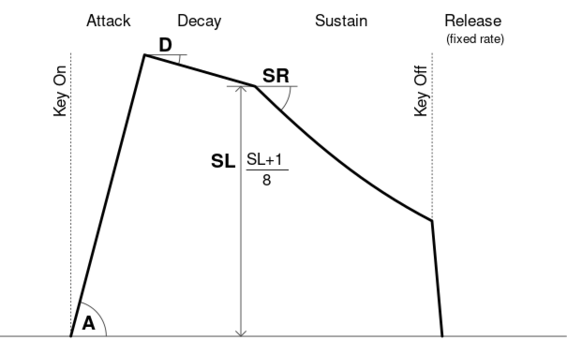
The ADSR describes a 4 stage envelope:
- Attack begins at key-on, rising from 0 to full over a chosen amount of time.
- Decay lowers from full to a chosen Sustain Level.
- Sustain exponential decay from Sustain Level to 0 (if the Sustain Rate is non-zero).
- Release begins at key-off, lowering to 0 with an fixed decay.
See: S-SMP ADSR
| Name | Address | Bits | Notes |
|---|---|---|---|
| ADSR (1) | $X5 | EDDD AAAA | ADSR enable (E), decay rate (D), attack rate (A). |
| ADSR (2) | $X6 | LLLR RRRR | Sustain level (SL), sustain rate (SR). |
At a rate according to the period table the following action is performed, and the envelope is clamped to 0-2047 ($7FF):
- Attack at period[A*2+1]: adds 32, or if A=$F adds 1024 ($400).
- Decay at period[D*2+16]: envelope -= 1, then envelope -= envelope >> 8.
- Sustain at period[SR]: envelope -= 1, then envelope -= envelope >> 8.
- Release: envelope -= 8 every sample.
This table of timings gives the resulting time taken by the above operations:
- Attack is the time from 0 to full.
- Decay is the time from full to sustain level.
- Sustain is the time from full to 0.
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Gain Timings
See: S-SMP GAIN
| Name | Address | Bits | Notes |
|---|---|---|---|
| GAIN | $X7 | 0VVV VVVV 1MMV VVVV |
Mode (M), value (V). |
At a rate according to the period table the following action is performed, and the envelope is clamped to 0-2047 ($7FF):
- Linear gain adds or subtracts 32.
- Bent gain adds 32 if below 1536 ($600), or 8 if above.
- Exponential is two steps: envelope -= 1, then: envelope -= envelope >> 8.
This table gives times taken between 0 volume and full volume (or the reverse):
| GAIN | |||||||
|---|---|---|---|---|---|---|---|
| Decrease Linear | Decrease Exponential | Increase Linear | Increase Bent | ||||
| V | Time (ms) | V | Time (ms) | V | Time (ms) | V | Time (ms) |
| $80 | Infinite | $A0 | Infinite | $C0 | Infinite | $E0 | Infinite |
| $81 | 4100 | $A1 | 38000 | $C1 | 4100 | $E1 | 7200 |
| $82 | 3100 | $A2 | 28000 | $C2 | 3100 | $E2 | 5400 |
| $83 | 2600 | $A3 | 24000 | $C3 | 2600 | $E3 | 4600 |
| $84 | 2000 | $A4 | 19000 | $C4 | 2000 | $E4 | 3500 |
| $85 | 1500 | $A5 | 14000 | $C5 | 1500 | $E5 | 2600 |
| $86 | 1300 | $A6 | 12000 | $C6 | 1300 | $E6 | 2300 |
| $87 | 1000 | $A7 | 9400 | $C7 | 1000 | $E7 | 1800 |
| $88 | 770 | $A8 | 7100 | $C8 | 770 | $E8 | 1300 |
| $89 | 640 | $A9 | 5900 | $C9 | 640 | $E9 | 1100 |
| $8A | 510 | $AA | 4700 | $CA | 510 | $EA | 900 |
| $8B | 380 | $AB | 3500 | $CB | 380 | $EB | 670 |
| $8C | 320 | $AC | 2900 | $CC | 320 | $EC | 560 |
| $8D | 260 | $AD | 2400 | $CD | 260 | $ED | 450 |
| $8E | 190 | $AE | 1800 | $CE | 190 | $EE | 340 |
| $8F | 160 | $AF | 1500 | $CF | 160 | $EF | 280 |
| $90 | 130 | $B0 | 1200 | $D0 | 130 | $F0 | 220 |
| $91 | 96 | $B1 | 880 | $D1 | 96 | $F1 | 170 |
| $92 | 80 | $B2 | 740 | $D2 | 80 | $F2 | 140 |
| $93 | 64 | $B3 | 590 | $D3 | 64 | $F3 | 110 |
| $94 | 48 | $B4 | 440 | $D4 | 48 | $F4 | 84 |
| $95 | 40 | $B5 | 370 | $D5 | 40 | $F5 | 70 |
| $96 | 32 | $B6 | 290 | $D6 | 32 | $F6 | 56 |
| $97 | 24 | $B7 | 220 | $D7 | 24 | $F7 | 42 |
| $98 | 20 | $B8 | 180 | $D8 | 20 | $F8 | 35 |
| $99 | 16 | $B9 | 150 | $D9 | 16 | $F9 | 28 |
| $9A | 12 | $BA | 110 | $DA | 12 | $FA | 21 |
| $9B | 10 | $BB | 92 | $DB | 10 | $FB | 18 |
| $9C | 8 | $BC | 74 | $DC | 8 | $FC | 14 |
| $9D | 6 | $DD | 55 | $BD | 6 | $FD | 11 |
| $9E | 4 | $BE | 37 | $DE | 4 | $FE | 7 |
| $9F | 2 | $BF | 18 | $DF | 2 | $FF | 3.5 |
Period Table
The rate of DSP envelope events are controlled by a common table of 32 periods. Each entry is how many S-SMP clocks elapse per envelope operation. The table is arranged in groups of 3.
Additionally, each column of periods appears to have a delay offset applied to it, affecting when the operation occurs. If counter is counting down the number of S-SMP clocks elapsed since reset, the envelope operation is applied when the following is true:
- 0 == (counter + offset[rate]) % period[rate]
The counter begins at 0 after reset, and decrements on each S-SMP clock, wrapping to $77FF (30,720) when it would go below 0[1]. (The first clock after reset will wrap.)
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Note that most of the offsets given above are effectively much smaller, given that they are modulo (%) with their associated period, but the modulo-equivalent larger values shown here demonstrate the symmetry between columns.
References
- ↑ apudsp_jwdonal.txt - Anomie's S-DSP document.